KimHwon

www.acmicpc.net/problem/2125

kimhwon.tistory.com/27 와 매우 유사한 문제. 다만 원 대신 볼록 다각형이 등장한다.

시점과 종점이 주어지고, 여러 개의 볼록 다각형이 주어진다. 볼록 다각형들의 내부를 지나지 않으면서 종점에 도착하고자 할 때 최단 경로의 길이 (또는 불가능한지)를 구하면 된다. 단, 여기서 볼록 다각형의 내부란 모서리를 포함하지 않는다.

위 문제에서와 같은 전략으로 모든 꼭짓점들과 시점, 종점을 잇는 선분을 모두 만든다. 만든 선분이 모든 볼록 다각형의 외부에 있다면 사용 가능한 선분이다. 사용 가능한 선분으로 이루어진 그래프에서 최단 경로를 구하면 된다.

선분이 볼록 다각형의 내부/외부에 있는지 판정이 매우 까다롭지만, 총 4가지 경우로 분류할 수 있다.

1. 선분의 끝점과 다각형의 모서리가 만나는 경우
2. 선분의 끝점과 다각형의 꼭짓점이 만나는 경우
3. 선분의 중간과 다각형의 꼭짓점이 만나는 경우
4. 선분의 중간과 다각형의 모서리가 만나는 경우

네 번째 경우는 선분 교차 판정으로 간단하게 구할 수 있다.(bool intersect(const Line& a, const Line& b))  만약 교차한다면 선분이 다각형 내부에 있음이 자명하다.
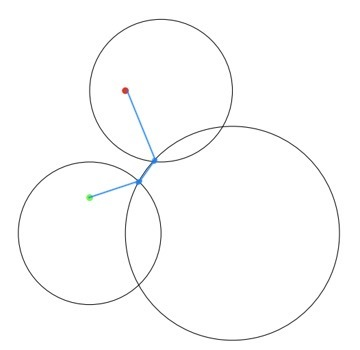
나머지 세 경우는 그림으로 정리했다.

파란 선은 확인하려는 선분, 검은 선은 다각형의 모서리, 초록과 빨간 선은 CCW 상태로 CCW면 초록색, CW면 빨간색이다. 선분 하나에 대하여, 모든 다각형의 모든 모서리를 순회하면서 위의 4가지 조건을 다 확인하면 된다.

코드

논리적으로 이렇게 하면 맞아야 정상이겠지만... 예제 중에 볼록다각형이 아닌 테케가 하나 있다. 게시판에 글을 쓰긴 했으나 아직 반영되진 않았다. 직접 출처인 SEERC 2005에서 데이터를 받아서 확인해보니, 미세하게 안쪽으로 파고든 점이 하나 있는 다각형이 있었다. 이를 예외처리하기 위해, 선분의 중점을 잡고 그 중점이 모든 다각형의 안쪽에 있는지도 판정했다. 수정 요청이 반영되었으며, 재채점까지 완료되었다.

https://www.acmicpc.net/problem/13466

시작점과 정수 N, R개의 직선이 주어진다. 시작점에서 직선을 따라 가다가 교차점을 만나면 오른쪽으로 돈다. N번 회전을 했을 때 어느 직선에 있는지 찾는 문제다.

N이 10^10이나 되기 때문에 단순한 시뮬레이션은 어려울 것처럼 보인다. 그런데 직선이 100개로 매우 적기 때문에 같은 교차점을 계속 순회할 것이라고 추측해 볼 수 있다.

잘 생각해 보면 교차점에서 무조건 오른쪽으로만 회전하므로 지나간 경로는 볼록다각형 형태로 나타날 것이다. 100개의 직선으로 만들 수 있는 꼭짓점이 가장 많은 볼록다각형 즉, 최대한 다양한 교차점을 지나는 경로는 100각형 형태다. 따라서 최대 100개의 교차점만 지나간다는 뜻이고, 시작점으로 돌아올 때까지만 시뮬레이션을 할 수 있다.

R이 작으므로 O(R^2)으로 각 직선끼리의 교점을 다 구한다. 각 직선마다 어느 지점에서 누구와 교차하는지 저장해 두고, 그 교점으로 정렬해두면 쉽게 구현할 수 있다.(vector<Cross> adj[]) lower_bound() 또는 upper_bound()를 잘 활용하면 어떤 직선에서 교점을 알 때, 그 교점에 바로 왼쪽이나 오른쪽으로 인접한 다른 교점을 O(log(R))에 찾을 수 있다.(Cross getNext(const Cross& me, int& dir)) 찾은 새로운 교점에 연결된 다른 직선에 대하여, 같은 방식으로 인접한 또다른 교차점을 찾아 나가면 된다. 시작한 직선으로 돌아올 때까지를 한 사이클이라고 하면, 사이클의 N % (사이클 길이) 번째 직선이 답이다.

모든 교점에 대하여 인접한 교점을 찾는데 총 O(R log(R))이지만 맨 처음에 모든 직선에 대한 교점을 만드는데 O(R^2)이므로, O(R^2)으로 해결할 수 있다.

코드

www.acmicpc.net/problem/15004

시점과 종점, 여러 원들이 주어진다. 시점에서 원 내부만 지나면서 종점에 도착하고자 할 때 최단 경로의 길이 (또는 불가능한지)를 구하면 된다.

일단 자명한 점은 시점에서 종점으로 직선으로 가는 경우가 아니라면 최단경로는 무조건 원과 원 사이 교점을 지나야 한다는 것이다. 문제에 제시된 그림에 메모했다. (파랑)

잘 생각해보면 코너를 돌 때 최단으로 이동하는 방법은 코너에 최대한 붙어서 이동하는 것이다. 즉, 코너가 되는 지점인 교점을 지나쳐야 한다.

N이 25밖에 되지 않으므로 원들 사이 모든 교점을 구하고, 각 교점들과 시점, 종점을 모두 잇는 선분을 만든다. 선분을 따라 이동하는 최단 경로를 다익스트라 등으로 구할 수 있다. 여기서 각 선분이 가능한지 즉, 원 바깥으로 나가지 않는지 판정하는 것이 중요하다.

원과 원 사이 교점을 구하는 식은 여기를 참고하여 O(N^2)으로 모든 원 사이에 교점들을 다 찾았다.(tuple<int, Point, Point> intersect(Circle c1, Circle c2) 함수) 다시 N^2 = M개의 각 교점들을 O(M^2)으로 선분을 만들어보고 가능한지 체크한다.(bool incLine(Line ln, vector<Circle> &cir) 함수) 주의할 점은 시점에서 교점으로, 또는 종점에서 교점으로, 시점에서 종점으로 바로 갈 수도 있으므로 시점과 종점도 포함해서 생각해야 한다. 선분을 만들 수 있다면, 그래프에 간선으로 추가하고 다익스트라를 사용해서 최단 경로를 찾는다.(ld dijkstra(ll start, ll end))

최종적으로 시간복잡도는 O(ElogV)인데, 여기서 E = M^2 = N^4, V = N^2 이므로 O(N^4 log N)이다.

코드